Article 29

Characterizations of VB*G ∩ (N)

Real Analysis Exchange 23 (1997/8), no. 2, 571-600.

Mathematical reviews subject classification: 26A45, 26A46.

Abstract

The purpose of this paper is to give some characterizations of VB*G ∩ (N) on an arbitrary real set.

In (PVB) functions and integration (J. Austral. Math. Soc. (Series A) 36 (1984), 335-353), Sarkhel and Kar introduced the class (PAC), showing that it is equivalent to the class [VBG] ∩ (N) on a closed set.

In Article 28 we showed that the class (PAC)G (generalized (PAC)) is equivalent to VBG ∩ (N) on an arbitrary set.

In this paper, we introduce condition (PAC*), that is a slight modification of (PAC) (we replace expressions like |f(a)-f(b)| by the oscillation of the function f on the interval [a,b]).

Clearly the class (PAC*) is contained in (PAC). Thus we obtain the main result:

A function f:[a,b] → R is VB*G ∩ (N) on a subset E of [a,b], if and only if f ∈ (PAC*) on E.

(See Theorem 4.)

Consequently:

The set {f:[a,b] → R : f∈ VB*G ∩ (N) on E} is an algebra, whenever E is a subset of [a,b].

(See Corollary 3.)

In Theorem 1 we obtain the following result:

A function f:[a,b] → R is VB*G on a Lebesgue measurable subset E of [a,b] if and only if it is so on any null subset of E.

As a consequence of Theorems 1 and 4, we find seven characterizations of VB*G ∩ (N) on a Lebesgue measurable set (see Theorem 5).

In Theorem 2 we obtain the following result:

A function f:[a,b] → R is AC*G on a Lebesgue measurable subset E of [a,b] if and only if it is so on any null subset of E.

Using Theorems 1 and 2, we find fifteen characterizations of the class of AC*G functions on a closed set E, that are continuous at each point of E (see Theorem 6).

In the last two sections we study the relationship between Thomson's outer measure $\small{\mathcal S}_o-\mu_f$ and VB*G ∩ (N) on a Lebesgue measurable set.

In Theorem 8 we obtain that:

If f:[a,b] → R is VB*G and continuous at each point of a set A ⊆ [a,b] then m*(f(A)) = 0 if and only if 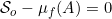$\small{\mathcal S}_o-\mu_f(A)=0$ .

Using this theorem we obtain again that:

The set {f:[a,b] → R : f \in VB*G ∩ (N) on E} is an algebra, whenever E is a subset of [a,b].

(See Corollary 8.) We also obtain the following characterization:

A function f:[a,b] → R is VB*G ∩ (N) on a Lebesgue measurable subset E of [a,b] if and only if there is a countable subset E₁ of E such that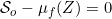 $\small{\mathcal S}_o-\mu_f (Z) = 0$ whenever Z is a null subset of E \ E_1.

(See Theorem 9.)

As a consequence of Theorem 9, it follows that:

A function f:[a,b] → R is AC*G on a closed subset E of [a,b] and continuous at each point of E if and only if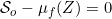 $\small{\mathcal S}_o-\mu_f (Z) = 0$ whenever Z is a null subset of E.

(See Theorem 10.)

Using different techniques, this result was obtained before in Article 17, Real Functions - Current Topics and rediscovered by Bongiorno, Di Piazza and Skvortsov in A new full descriptive characterization of Denjoy - Perron integral (Real Analysis Exchange 21 (1995/6), no. 2, 656--663).