Article 28

Characterizations of VBG ∩ (N)

Real Analysis Exchange 23 (1997/8), no. 2, 611-630.

Mathematical reviews subject classification: 26A45, 26A46, 26A39.

Abstract

The purpose of this paper is to give some characterizations of VBG ∩ (N) on an arbitrary real set.

In (PVB) functions and integration (J. Austral. Math. Soc. (Series A) 36 (1984), 335-353), Sarkhel and Kar introduced the class (PAC), showing that it is contained in [VBG] ∩ (N) and it is an algebra on any real set.

Moreover, (PAC) is equivalent to the class [VBG] ∩ (N) on a closed set. It is clear now that (PAC)G (generalized (PAC)) is contained in VBG ∩ (N).

Surprisingly, the converse is also true: we show that VBG ∩ (N) is equivalent with (PAC)G on an arbitrary real set, hence VBG ∩ (N) is an algebra on that set.

In fact in Theorem 4, we give three characterizations for VBG ∩ (N) on an arbitrary real set.

It follows that Gordon's AK_N-integral (see Some comments on an approximately continuous Khintchine integral, Real Analysis Exchange 20 (1994/5), no. 2, 831-841) is a special case of the PD-integral (The proximally continuous integrals, J. Austral. Math. Soc. (Series A) 31 (1981), 26-45) of Sarkhel and De (see Remark 3).

In Theorem 3 we obtain the following surprising result:

A Lebesgue measurable function f is VBG on a set E if and only if f is VBG on any null subset of E.

As a consequence of Theorems 3 and 4, we find seven characterizations of VBG ∩ (N) for Lebesgue measurable functions (see Theorem 5).

One of them asserts that:

A Lebesgue measurable function f is VBG ∩ (N) on a set E if and only if f is VBG ∩ (N) on any null subset of E.

For continuous functions on a compact set, we obtain several characterizations of the class ACG, such as:

A continuous function f is ACG on a compact set E if and only if f is (PAC)G on any null subset of E.

(See Corollary 4).

In the last two sections, we give five enhancements of V(f;E) (the ordinary variation of a function f on a set E):

$\small\nu_f^1(E)}\,, ~ \nu_f^2(E)\,, ~ \nu_f^3(E)\,, ~\nu_f^4(E)$ and $\small\nu_f^5(E)$ .

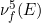For each of these set-functions we obtain another characterization of VBG ∩ (N) for a Lebesgue measurable function (see Theorem 8):

A Lebesgue measurable function f:E → R is VBG ∩ (N) if and only if for every null subset Z of E, there is a sequence {Z_n}_n whose union is Z, such that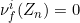 $\small\nu_f^i(Z_n) = 0$ for each n.