Article 38

On an improvement of a recent result of Thomson

Real Analysis Exchange 25 (1999/2000), no. 1, 429-436.

Mathematical reviews subject classification: 26A45, 26A39, 28A12.

Abstract

In σ-finite Borel measures on the real line (Real Analysis Exchange 23 (1997/8), no. 1, 185-192), Brian S. Thomson proved the following result:

Let f be AC*G on an interval [a,b]. Then the total variation measure μ = μ_f associated with f has the following properties:

1. μ is a σ-finite Borel measure on [a,b];
2. μ is absolutely continuous with respect to Lebesgue measure;
3. There is a sequence of closed sets F_n whose union is all of [a,b] such that μ (F_n) < ∞ for each n;
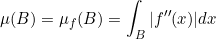4. $\small\mu(B) = \mu_f(B) =\int _B |f''(x)| dx$ for every Borel set B ⊂ [a,b].

Conversely, if a measure μ satisfies conditions a -c then there exists an AC*G function f for which the representation d) is valid.

In this paper we improve Thomson's theorem as follows:

In the first part we ask f to be only VB*G ∩ (N) on a Lebesgue measurable subset P of [a,b] and continuous at each point of P;
the converse is also true even for μ defined on the Lebesgue measurable subsets of P (see Theorem 2 and the two examples in Remark 1).