On an improvement of the Hake theorem
Real Analysis Exchange 24 (1998/9), No. 2, 867-872.
Mathematical reviews subject classification: 26A39, 26A42, 26A46.
Abstract
The well-known Hake Theorem asserts that:
If a function f is Denjoy* integrable then it is also Perron integrable, and the two integrals are equal.
In fact these two integrals are equivalent (see the Hake-Alexandroff-Looman Theorem), and there are many definitions of Perron-type integrals that are equivalent to the Denjoy* integral.
In Corollary 5.9.1 of Real Functions - Current Topics we made a study of many (at least 108) of these equivalences.
One of the strongest Perron type definition is that of Skljarenko, where the major and minor functions are AC*G and continuous.
Using the Tolstoff-Zahorski Theorem we showed that in addition, the major and minor functions have finite or infinite derivatives at each point, obtaining the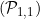
-integral.
To prove that the Denjoy*-integrability implies the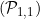 - integrability (i.e., a Hake type theorem) we used essentially the Vitali-Caratheodory Theorem (see I. P. Natanson, Theory of functions of a real variable, 2nd. rev. ed., Ungar, New York, 1961, p. 166).
In the present paper we give a different, less technical proof of this result, using essentially Lusin's Theorem (see S. Saks, Theory of the integral, 2nd. rev. ed., vol. PWN, Monografie Matematyczne, Warsaw, 1937, p. 72).
Both proofs use different techniques from that of Skljarenko.
We conclude the paper with some comments and a question related to the subject.
