Article 36

Thomson's variational measure

Real Analysis Exchange 24 (1998/9), No. 2, 523-566.

Mathematical reviews subject classification: 26A45, 26A46, 26A24.

Abstract

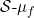For a local system $\small{\mathcal S}$ and a function f:R → R, Thomson defines (see B. S. Thomson, Real functions, Lect. Notes in Math., 1170, Springer-Verlag, 1985) the metric outer measure $\small{\mathcal S}\text{-}\small\mu _f$ on R.

We introduced in Real Functions - Current Topics the properties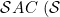 $\small{\mathcal S}AC ~({\mathcal S}$ -absolute continuity) and $\small{\mathcal S}ACG$ .

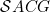In this paper we show that for some particular local systems, such as 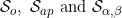$\small {\mathcal S}_o, ~{\mathcal S}_{ap}~ \text{and}~ {\mathcal S}_{\alpha ,\beta }\:$ , there is a strong relationship between $\small{\mathcal S}\text{-}\mu _f~ \text{and} ~{\mathcal S}ACG$ .

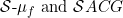For example (see Theorem 8.4):

A function f:[a,b] → R is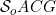 $\small{\mathcal S}_oACG$ on a Lebesgue measurable set E \subset [a,b]

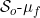⇒ $\small{\mathcal S}_o\text{-}\mu_f$ is absolutely continuous on E

⇒ f is VB*G ∩ (N) on E and f is continuous at each point of E

In Theorem 5.1, we show that:

A function f:[a,b]→ R, Lebesgue measurable on E ⊆ [a,b], is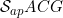 $\small {\mathcal S}_{ap}ACG$ on E if and only if 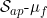$\small {\mathcal S}_{ap}\text{-}\mu _f$ is absolutely continuous on E.

This result remains true if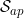 $\small{\mathcal S}_{ap}$ is replaced by 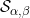$\small{\mathcal S}_{\alpha ,\beta }$ with $\small\alpha ,\beta \in \bigl(1/2\,,\,1\bigr]$ (see Theorem 5.1).

We also give several characterizations of the VB*G functions on an arbitrary set, that are continuous at each point of that set (see Theorem 7.4).