The wide Denjoy integral as a limit of a sequence of stepfunctions in a suitable convergence
Real Analysis Exchange 23 (1997/8), no. 2, 719-734.
Mathematical reviews subject classification: 26A39, 26A46.
Abstract
E. J. McShane (Integration, Princeton University Press, Princeton, 1944) and F. Riesz and B. Sz-Nagy (Leçons d'analyse fonctionelle, 3nd. ed., Akad. Kiado, Budapest, 1955) developed the Lebesgue integration on an interval I ⊂ Rn using the monotone convergence of stepfunctions.
In A Riesz-type definition of the Denjoy integral (Real Analysis Exchange 11 (1985-1986), 221-227), Lee and Chew showed that a function f:[a,b] → R that is Denjoy*-integrable on [a,b] can be defined as the limit of a controlled convergent sequence of stepfunctions.
However, their proof is not complete.
That this result is indeed true is shown by us in Article 24.
In a recent paper Kurzweil and Jarnik (Perron type integration on n-dimensional intervals as an extension of integration of stepfunctions by strong equiconvergence, Czech. Math. J. 46 (1996), no. 121, 1-20) proved an analogue result of Lee and Chew for the multidimensional case.
For the one-dimensional case, we shall prove that a function f:[a,b] → R that is Denjoy-integrable on [a,b] can be defined as the limit of a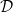
-controlled convergent sequence of stepfunctions (see the second part of Theorem 2).
In the last section we show that Ridder's α- and β-integrals can be defined as the limit of controlled convergent sequences of stepfunctions (see Theorem 4).
The results in this paper are heavily based on Lemma 3, and its proof uses a technique that seems to be new (see Remark 3).
