Article 34

On the decomposition theorems of Lebesgue and Jordan

Real Analysis Exchange 23 (1997/8), no. 1, 313-324.

Mathematical reviews subject classification: 26A45, 26A46, 26A48.

Abstract

The following decomposition theorem of Lebesgue is well known:

Theorem A : Lebesgue's decomposition theorem

(S. Saks, Theory of the integral, 2nd. rev. ed., vol. PWN, Monografie Matematyczne, Warsaw, 1937).

If F is an additive function of bounded variation of an interval, the derivative F' is summable, and the function F is the sum of a singular additive function of an interval and of the indefinite integral of the derivative F'. Moreover, if the function F is non-negative, we have for every interval I_o

$\small\displaystyle F(I_o) \ge \int_{I_o} F'(t) dt$ ,

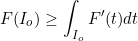equality holding only in the case in which the function F is absolutely continuous on I_o.

In the first part of this paper, for the special case of a function defined on an interval [a,b], with bounded variation and satisfying Lusin's condition (N), Theorem A becomes

$\small \displaystyle F(x) - F(a) = s_F(x) + ({\mathcal L}) \int_a^x F'(t) dt$ ,

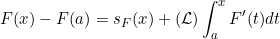where s_F is the saltus function of F (clearly s_F is a singular function).

Moreover we obtain

$\small \displaystyle V\bigl (F;[a,x]\bigr ) = S_F(x) + ({\mathcal L}) \int_a^x |F'(t)| dt$

(for the definition of S_F see Lemma 8).

The following decomposition theorem of Jordan is well known:

Theorem B.: Jordan's decomposition theorem

(I. P. Natanson, Theory of functions of a real variable, 2nd. rev. ed., Ungar, New York, 1961, p. 218)

A function F:[a,b] → R is VB if and only if it is representable as the difference of two increasing functions.

In fact from the proof of this theorem it follows that if F is VB on [a,b] then the functions V_F(x):= V(F,[a,x]) and G(x): = F(x) - V_F(x) are increasing.

The question is which properties of F will be preserved for V_F and G?

It is known that if F is left, right or bilaterally continuous at a point x ∈ [a,b] then so are V_F and G (see I. P. Natanson, Theory of functions of a real variable, 2nd. rev. ed., Ungar, New York, 1961, p. 223).

In the second part of this paper we show that if F satisfies Lusin's condition (N) then V_F and G also satisfy (N).