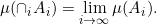Article 31

An elementary proof of the Banach-Zarecki theorem

Real Analysis Exchange 23 (1997/8), no. 1, 295-302.

Mathematical reviews subject classification: 26A45, 26A46, 26A48.

Abstract

There is a very rich literature concerning the Banach-Zarecki Theorem, such as the books of Saks (Theory of the integral, 2nd. rev. ed., vol. PWN, Monografie Matematyczne, Warsaw, 1937, p. 227), Natanson (Theory of functions of a real variable, 2nd. rev. ed., Ungar, New York, 1961, p. 250), Foran (Fundamentals of real analysis, Marcel Dekker Inc, New York, Basel, Hong Kong, 1991, p. 357), Ene (Real Functions - Current topics, pp. 81, 104) and a paper of Varberg (On absolutely continuous functions, Amer. Math. Monthly 72 (1965), p. 835).

This theorem asserts that:

If a continuous and VB function satisfies Lusin's condition (N) on an interval then it is also AC on that interval.

The proofs of Saks, Foran, Varberg and Ene (p. 81) are based on the following result (see Theorem 6.5 of Saks, p. 227; Theorem of Foran; Theorem 1 of Varberg , p. 834 ):

If a function F is derivable at every point of a measurable set D, then

$\small m^*(F(D)) \le (\mathcal L) \int_D |F'(x)| dx$ .

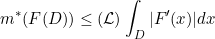In Natanson's book, the Banach-Zarecki Theorem is proved in a totally different way, namely using Lebesgue's Convergence Theorem as well as the fact that the Banach indicatrix for a continuous and VB function on [a,b] is summable (see Theorem 3 of Natanson, p. 225).

In Real Functions - Current Topics (p. 104), the Banach-Zarecki Theorem is a consequence of some general notions (AC_∞, VB_∞ etc.). Here the Banach indicatrix has also an important role, but the proof is different from that in Natanson's book.

In this paper we shall give a new, elementary proof of the Banach-Zarecki theorem, based on the following classical result (see Foran's book, p. 183):

If {A_i}_i is a sequence of decreasing sets in a measurable space (X, M,μ) and μ(A₁) < +∞ then

$\small \displaystyle \mu (\cap_i A_i) = \lim_{i \to \infty} \mu (A_i).$