Article 27

Riesz type theorems for general integrals

Real Analysis Exchange 22 (1997), no. 2, 714-733

Mathematical reviews subject classification: 26A39, 26A46, 26A45, 46A50, 54E52.

Abstract

The author gives a general descriptive definition for integration, denoted by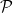 $\small{\mathcal P}$ , which has as special cases

the Lebesgue integral for bounded measurable functions,
the Lebesgue integral,
the Denjoy-Perron integral $\small{\mathcal D}^*$ ,
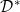the wide Denjoy integral $\small{\mathcal D}$ ,
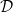the Foran integral,
the Iseki integral and
the 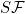$\small S{\mathcal F}$ -integral

(see Real Functions - Current Topics).

This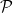 $\small{\mathcal P}$ -integral will admit Riesz type representation theorems (introducing an Alexiewicz norm, and identifying f with g whenever f = g a.e. on [a,b]).

As a consequence of Theorem 2, it follows the classical Riesz representation theorem for the linear and continuous functionals on (C([a,b]),||· ||_∞).

In addition it is shown that the space of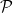 $\small{\mathcal P}$ - integrable functions is of the first category in itself (see Section 5).

Also a characterization of the weak convergence on this space is given.