Article 22

A note on an assumption of P. Y. Lee and T. S. Chew

Real Analysis Exchange 21 (1995-1996), no.2, 755-757.

Mathematical reviews subject classification: 26A39; 26A24.

Abstract

The aim of this article is to prove the following assertion (see Corollary 1):

Let F:[a,b] → R and let E_i, i = {1,n} be closed subsets of [a,b].

Let F_n:[a,b] → R, such that

F_n(x) = F(x), for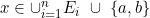 $\small x \in \cup_{i=1}^n E_i ~\cup~ \{a,b\}$ and

F_n is linear on the closure of each interval contiguous to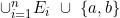 $\small \cup_{i=1}^n E_i ~ \cup~ \{a,b\}$ .

If F is continuous on [a,b] and F ∈ AC* on each E_i then F_n is derivable a.e. on [a,b] and F'_n is summable on [a,b].

In A Riesz-type definition of the Denjoy integral (Real Analysis Exchange 11 (1985/6), p.224) P.Y. Lee and T.S. Chew use this result essentially, without proof and without stating it explicitly, claiming that "it is easy to verify''.

The same result is also used by P.Y. Lee in Theorem 10.2 of Lanzhou lectures on Henstock integration (World Scientific, Singapore, 1989, p. 59).